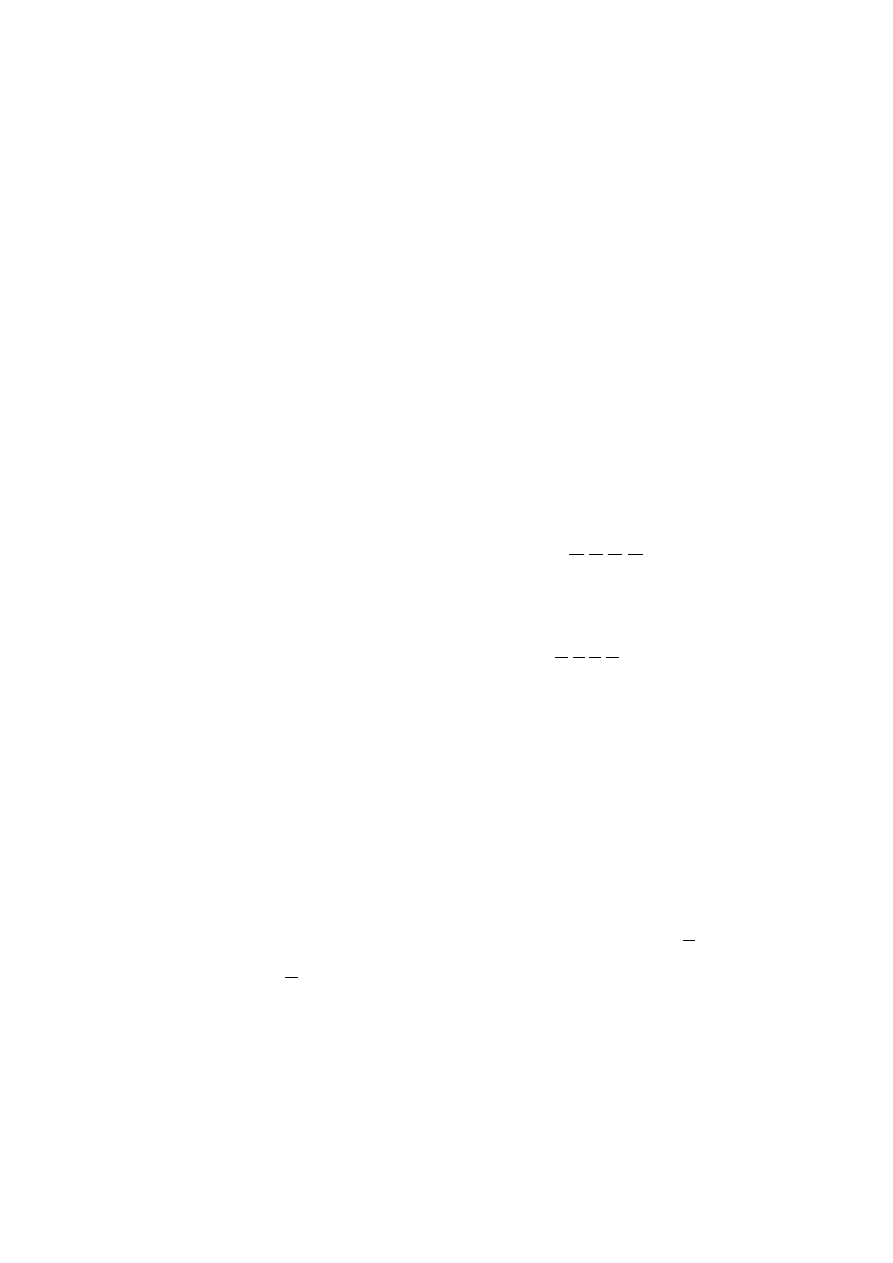
Badanie symetrycznego czwórnika

opracował Sebastian Broszkiewicz

Spis treści

I.

Podstawy teoretyczne ćwiczenia.

1. Pojęcia podstawowe dotyczące czwórnika.

2.

Równania czwórnika.

3.

Warunki symetrii i odwracalności czwórnika.

4.

Stany pracy czwórnika.

5.

Impedancja wejściowa czwórnika.

6.

Sens fizyczny parametrów łańcuchowych A,B,C,D.

7.

Czwórniki pasywne.

1) Schematy zastępcze czwórników pasywnych.

2) Wyznaczenie parametrów łańcuchowych A,B,C,D w funkcji

impedancji w stanie jałowym i w stanie zwarcia.

3) Impedancja charakterystyczna czwórnika symetrycznego.

2

2

3

5

7

7

8

9

9

12

14

II. Przebieg ćwiczenia.

1. Wyznaczenie parametrów czwórnika na podstawie znajomości

impedancji elementów jego struktury.

2.

Wyznaczenie parametrów czwórnika na podstawie znajomości

impedancji wejścia czwórnika w stanie biegu jałowego Z

o

i

zwarcia Z

k

.

15

15

17

III. Wnioski.

IV. Literatura.

18

18

I.

Podstawy teoretyczne ćwiczenia.

1. Pojęcia podstawowe dotyczące czwórnika.

Czwórnik jest elementem czterozaciskowym mającym dwie pary

uporządkowanych zacisków, z których jedną nazywamy wejściem a drugą

wyjściem (rys.1).

Rys.1.Schemat ogólny czwórnika

W odniesieniu do wejścia i wyjścia czwórnika musi być spełniony następujący

warunek równowagi prądów :

I

1

= I

1

’ ; I

2

= I

2

’

(I.1.1)

Wielkości związane z wejściem, a więc napięcie i prąd na wejściu czwórnika

opatrzone są wskaźnikiem 1, a wielkości związane z wyjściem wskaźnikiem 2.

Czwórniki dzielimy na liniowe i nieliniowe, stacjonarne i niestacjonarne,

symetryczne i niesymetryczne, odwracalne i nieodwracalne, pasywne

i aktywne.

Czwórnik nazywamy liniowym jeśli spełnia on własność addytywności

i jednorodności, czyli jeśli y

1

jest odpowiedzią układu na dowolne wymuszenie

u

1

, a y

2

jest odpowiedzią na dowolne wymuszenie u

2

, to y

1

+y

2

jest

odpowiedzią układu na wymuszenie u

1

+u

2

, oraz jeśli y jest odpowiedzią

układu na dowolne wymuszenie u, to ay jest odpowiedzią na wymuszenie au

(a – stała rzeczywista).

1

I

1

Wejście U

1

1’ I

1

’

I

2

2

U

2

Wyjście

I

2

’ 2’

2

Czwórnik nazywamy stacjonarnym jeśli jego parametry są niezależne od czasu.

Czwórnik nazywamy symetrycznym jeśli przy zmianie miejscami wejścia

z wyjściem, nie zmieni się rozpływ prądów i rozkład napięć w obwodzie poza

czwórnikiem, tzn. w obwodzie dołączonym do wejścia i wyjścia czwórnika.

Jeżeli do zacisków wejściowych czwórnika odwracalnego doprowadzimy

idealne źródło napięcia E, które w zwartym obwodzie wyjścia wywoła prąd I,

to po przemieszczeniu tego źródła do wyjścia, w zwartym obwodzie wejścia

też popłynie prąd I.

Czwórnik nazywamy pasywnym, jeśli dla dowolnej chwili t energia

doprowadzona do czwórnika jest nieujemna.

2. Równania czwórnika.

Równania czwórnika określają związki pomiędzy prądami i napięciami na

wejściu i wyjściu czwórnika. Ponieważ przedmiotem rozważań będą czwórniki

liniowe, zatem do rozwiązywania zagadnień można stosować metody

rozwiązywania obwodów.

Związki miedzy czterema wielkościami U

1

,U

2

,I

1

,I

2

ujmujemy za pomocą

dwóch równań liniowych. W zależności od charakteru współczynników

rozróżniamy sześć zasadniczych równań czwórnika :

a) równanie impedancyjna

U

1

i U

2

są wyrażone w zależności od I

1

i I

2

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

=

⎥

⎦

⎤

⎢

⎣

⎡

2

1

22

21

12

11

2

1

I

I

z

z

z

z

U

U

(I.2.1)

w którym : z

11

,z

12

,z

21

,z

22

– parametry impedancyjne, a

z -

⎥

⎦

⎤

⎢

⎣

⎡

=

22

21

12

11

z

z

z

z

macierz impedancyjna

b) równanie admitancyjne

I

1

i I

2

są wyrażone w zależności od U

1

i U

2

3

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

=

⎥

⎦

⎤

⎢

⎣

⎡

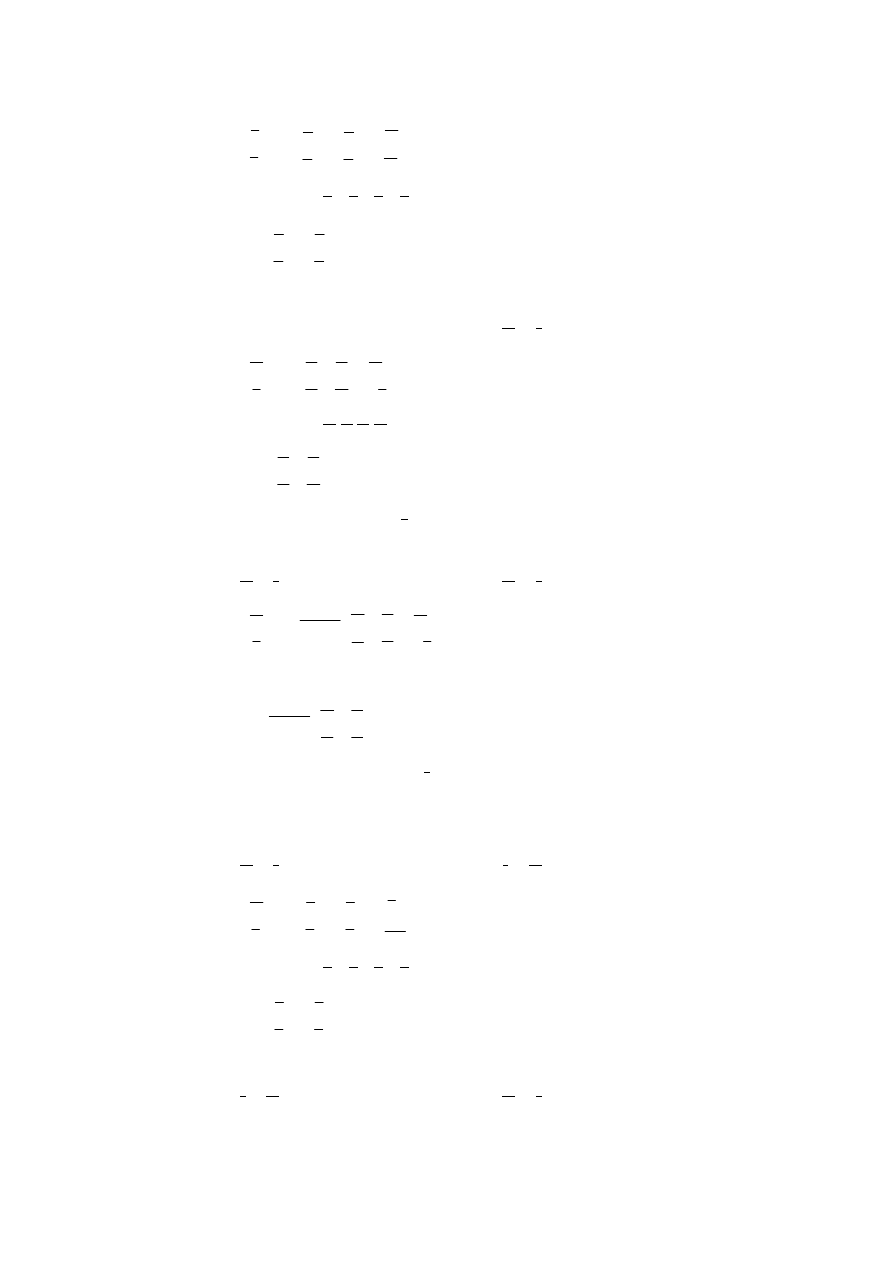
2

1

22

21

12

11

2

1

U

U

y

y

y

y

I

I

(I.2.2)

w którym : y

11

,y

12

,y

21

,y

22

– parametry admitancyjne, a

y

⎥

⎦

⎤

⎢

⎣

⎡

=

22

21

12

11

y

y

y

y

- macierz admitancyjna

c) równanie łańcuchowe proste

U

1

i I

1

są wyrażone w zależności od U

2

i I

2

⎥

⎦

⎤

⎢

⎣

⎡

−

⎥

⎦

⎤

⎢

⎣

⎡

=

⎥

⎦

⎤

⎢

⎣

⎡

2

2

1

1

I

U

D

C

B

A

I

U

(I.2.3)

w którym : A,B,C,D – parametry łańcuchowe, a

A

⎥

⎦

⎤

⎢

⎣

⎡

=

D

C

B

A

- macierz łańcuchowa

Znak „-” przy prądzie I

2

wynika ze strzałkowania tego prądu na rysunku 1.

d) równanie łańcuchowe odwrócone

U

2

i I

2

wyrażone są w zależności od U

1

i I

1

⎥

⎦

⎤

⎢

⎣

⎡

−

⎥

⎦

⎤

⎢

⎣

⎡

=

⎥

⎦

⎤

⎢

⎣

⎡

1

1

2

2

det

1

I

U

A

C

B

D

I

U

A

(I.2.4)

w którym

B

⎥

⎦

⎤

⎢

⎣

⎡

=

A

C

B

D

A

det

1

- macierz łańcuchowa odwrócona

Znak „-” przy prądzie I

2

wynika ze strzałkowania tego prądu jak na

rysunku 1.

e) równanie mieszane (hybrydowe)

U

1

i I

2

wyrażone są w zależności od I

1

i U

2

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

=

⎥

⎦

⎤

⎢

⎣

⎡

2

1

22

21

12

11

2

1

U

I

h

h

h

h

I

U

(I.2.5)

w którym : h

11

,h

12

,h

21

,h

22

– parametry hybrydowe, a

h

⎥

⎦

⎤

⎢

⎣

⎡

=

22

21

12

11

h

h

h

h

- macierz hybrydowa

f) równanie hybrydowe odwrócone

I

1

i U

2

wyrażone są w zależności od U

1

i I

2

4

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

=

⎥

⎦

⎤

⎢

⎣

⎡

2

1

22

21

12

11

2

1

I

U

g

g

g

g

U

I

(I.2.6)

w którym : g

11

,g

12

,g

21

,g

22

– parametry hybrydowe odwrócone, a

g

⎥

⎦

⎤

⎢

⎣

⎡

=

22

21

12

11

g

g

g

g

- macierz hybrydowa odwrócona

3. Warunki symetrii i odwracalności czwórnika.

W dotychczasowych rozważaniach zakładaliśmy zwrot prądów I

1

i I

2

do

„pudełka”. Często jednak, zwłaszcza w przypadku postaci łańcuchowej,

wygodnie jest przyjmować zwrot prądu zgodnie z kierunkiem przekazywania

energii, tzn. prąd I

1

do „pudełka”, a prąd I

2

od „pudełka”. Takie strzałkowanie

będzie wykorzystane w poniższych wyliczeniach.

W celu określenia warunków jakie musi spełniać czwórnik odwracalny,

załóżmy że czwórnik jest zasilany od strony zacisków wejściowych napięciem

U

1

=E, natomiast zaciski wyjściowe są zwarte (U

2

=0).Korzystając z równań w

postaci łańcuchowej :

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

=

⎥

⎦

⎤

⎢

⎣

⎡

2

2

1

1

I

U

D

C

B

A

I

U

lub

U

1

=A U

2

+ B I

2

;

I

1

=C U

2

+ D I

2

,

(I.3.1)

otrzymamy

U

1

=B I

2

,

(I.3.2)

stąd

I

2

=

E

B

U

B

1

1

1

=

(I.3.3)

Jeśli natomiast do czwórnika od strony zacisków wyjściowych zostanie

doprowadzone napięcie E=U

2

, a zaciski wejściowe są zwarte (U

1

=0), to

zgodnie z równaniem w postaci łańcuchowej odwróconej

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

−

−

=

⎥

⎦

⎤

⎢

⎣

⎡

1

1

2

2

det

1

I

U

A

C

B

D

I

U

A

, lub

U

2

=

1

1

det

det

I

B

U

D

A

A

−

;

I

2

=

1

1

det

det

I

A

U

C

A

A

+

−

(I.3.4)

5

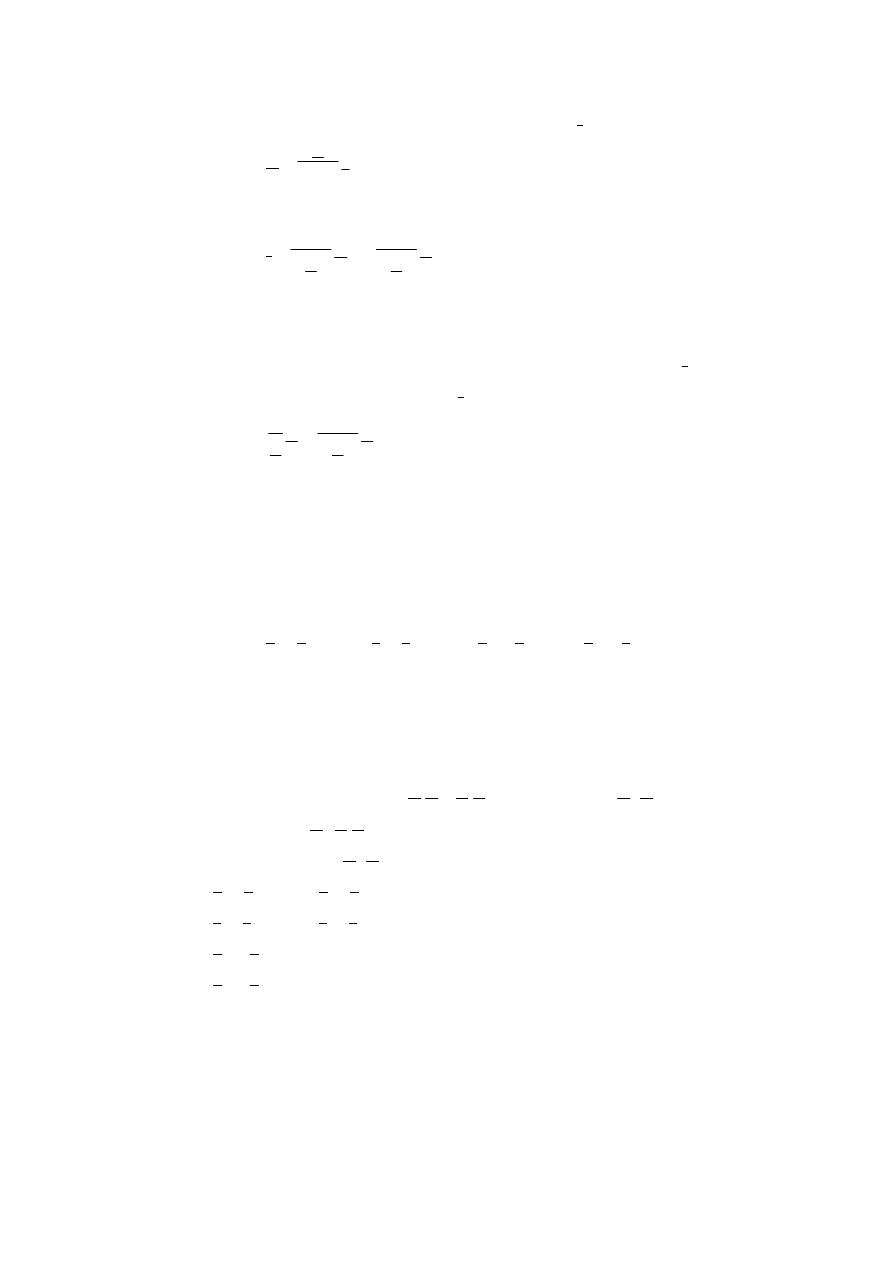
w zwartym obwodzie wejścia popłynie prąd (prąd I

1

zmieni swój zwrot)

U

2

=

1

det

I

B

A

,

(I.3.5)

stąd otrzymamy

I

1

=

E

B

U

B

A

A

det

det

2

=

(I.3.6)

Zasada wzajemności jest spełniona, jeśli wyznaczony prąd I

2

jest równy

wyznaczonemu powyżej prądowi I

1

:

E

B

E

B

A

det

1

=

stąd otrzymujemy warunek :

detA=1

który jest warunkiem odwracalności czwórnika.

Warunki odwracalności odpowiadające parametrom admitancyjnym,

impedancyjnym i hybrydowym są następujące:

y

12

=y

21

;

z

12

=z

21

;

h

12

=-h

21

;

g

12

=-g

21

Z definicji wyrażającej symetrię czwórnika wynika, że dla czwórnika

symetrycznego macierze A i B muszą być sobie równe. Porównując równanie

łańcuchowe i równanie łańcuchowe odwrotne stwierdzamy, że warunek ten jest

spełniony, jeśli przy detA=A D – B C=1, oraz parametr A=D.

Wtedy detA=A

2

-B C=1.

Jeśli detA=1 oraz A=D, to

y

11

=y

22

;

y

12

=y

21

z

11

=z

22

;

z

12

=z

21

h

12

=-h

21

;

deth=1

g

12

=-g

21

;

detg=1

Z powyższych zależności wynika że czwórniki symetryczne są również

odwracalne.

6

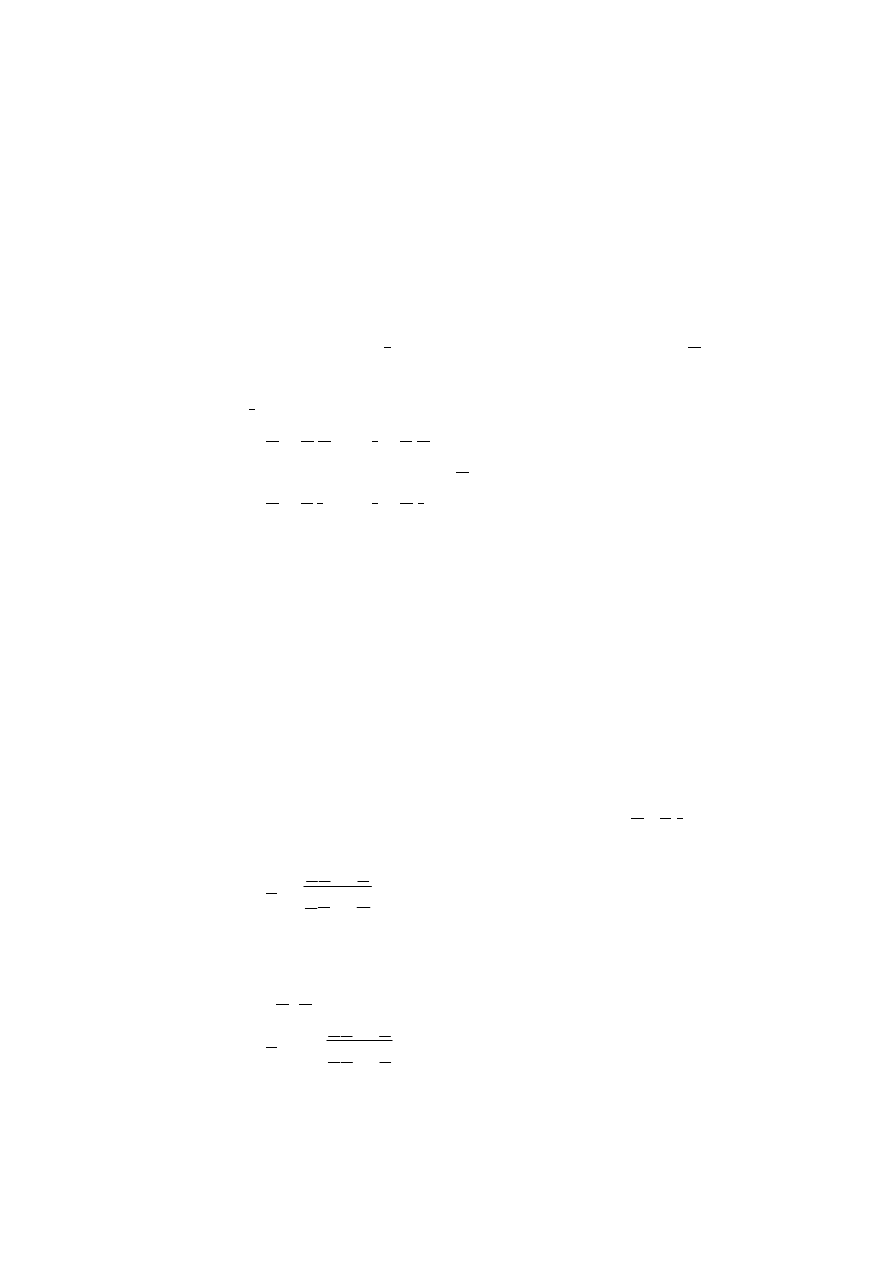
4. Stany pracy czwórnika.

Do zacisków wejściowych czwórnika przeważnie jest dołączone źródło

napięcia lub źródło prądu. Zaciski wyjściowe mogą być rozwarte i wtedy stan

pracy nazywamy stanem jałowym, mogą być zwarte i taki stan pracy to stan

zwarcia i do zacisków wyjściowych może być dołączony również odbiornik i

taki stan pracy nazywamy stanem obciążenia.

W stanie jałowym prąd I

2

=0, w stanie zwarcia natomiast napięcie U

2

=0

Biorąc pod uwagę równanie łańcuchowe stwierdzamy, że w stanie jałowym,

przy I

2

=0

U

10

=A U

20

; I

10

=C U

20

(I.4.1)

Natomiast w stanie zwarcia, przy U

2

=0

U

1k

=B I

2k

; I

1k

=D I

2k

(I.4.2)

Również równania impedancyjne, admitancyjne i hybrydowe ulegają

uproszczeniu w stanie jałowym i w stanie zwarcia.

5. Impedancja wejściowa czwórnika.

Stosunek napięcia na wejściu do prądu na wejściu nazywamy impedancją

wejściową czwórnika.

W zależności od stanu pracy czwórnika możemy wyznaczyć impedancję

wejściową w stanie obciążenia, w stanie jałowym i w stanie zwarcia.

Uwzględniając równania łańcuchowe i zakładając U

2

=Z

o

I

2

otrzymamy

impedancje wejściowa w stanie obciążenia

Z

we

=

D

Z

C

B

Z

A

o

o

+

+

(I.5.1)

Impedancja wejściowa czwórnika symetrycznego po uwzględnieniu warunku

symetrii A=D wyniesie

Z

we sym

=

A

Z

C

B

Z

A

o

o

+

+

(I.5.2)

Impedancję wejściową w stanie jałowym i w stanie zwarcia można określić na

podstawie równań z punktu 4 :

7

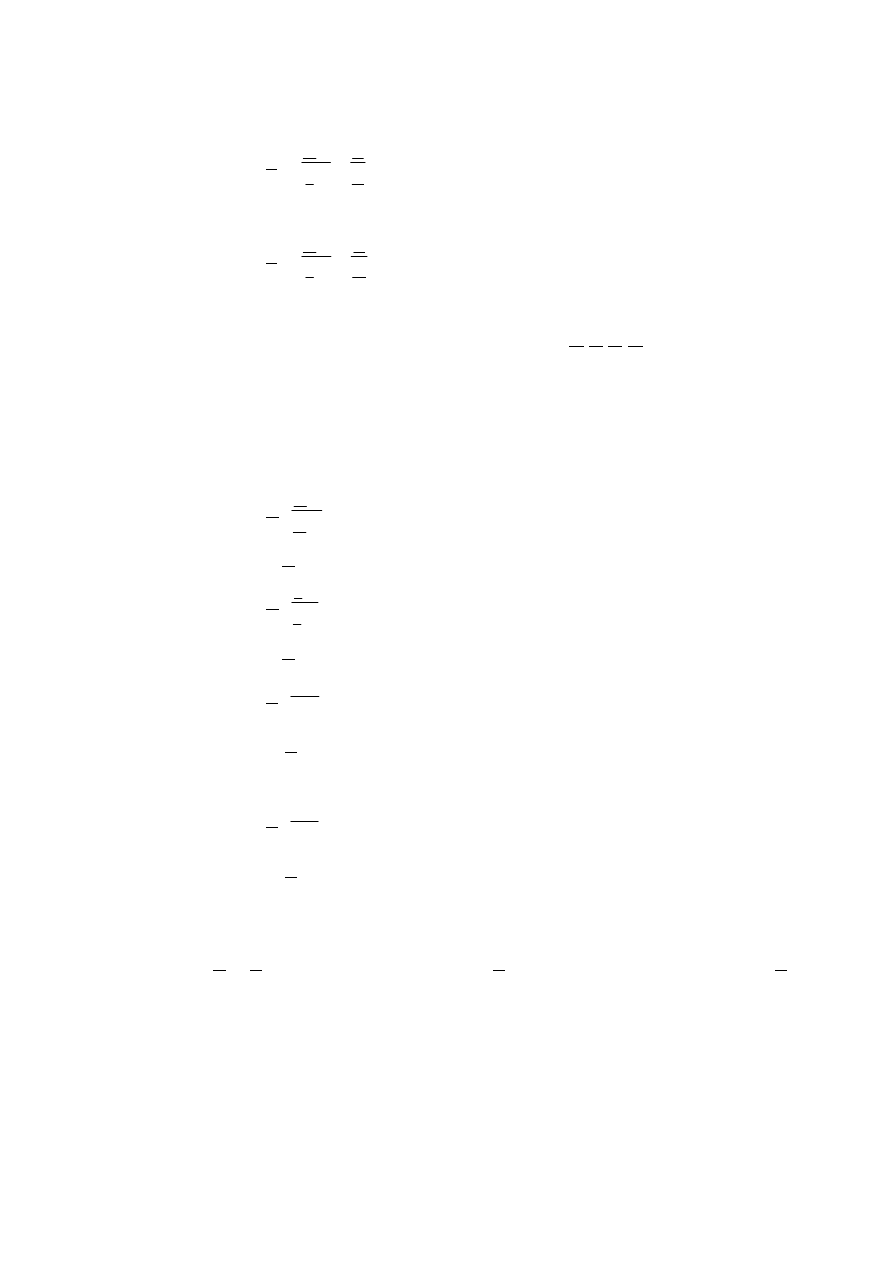
w stanie jałowym

Z

10

=

C

A

I

U

=

10

10

(I.5.4)

w stanie zwarcia

Z

1k

=

D

B

I

U

k

k

=

1

1

(I.5.5)

6. Sens fizyczny parametrów łańcuchowych A,B,C,D.

Na podstawie zależności dotyczących stanu jałowego i stanu zwarcia

czwórnika można podać sens fizyczny parametrów łańcuchowych. I tak

otrzymujemy :

A=

20

10

U

U

(I.6.1)

Parametr A jest więc równy przekładni napięć w stanie jałowym.

D=

k

k

I

I

2

1

(I.6.2)

Parametr D jest równy przekładni prądów w stanie zwarcia.

C=

20

10

U

I

(I.6.3)

Parametr C jest równy stosunkowi prądu na wejściu do napięcia na wejściu

w stanie jałowym.

B=

k

k

I

U

2

1

(I.6.4)

Parametr B jest równy stosunkowi napięcia na wejściu do prądu na wyjściu

w stanie zwarcia.

Z powyższych równań wynika wymiar parametrów łańcuchowych: parametry

A i B są bezwymiarowe, parametr C ma wymiar admitancji, parametr B

natomiast ma wymiar impedancji.

8

7. Czwórniki pasywne.

1) Schematy zastępcze czwórników pasywnych.

Spośród czterech parametrów macierzy łańcuchowej opisującej czwórnik

pasywny, trzy parametry ą w ogólnym przypadku niezależne, gdyż parametry

te spełniają równanie A D – B C = 1. W szczególnym przypadku czwórnika

symetrycznego dodatkowo A=D, a więc niezależne są dwa parametry.

Trzy parametry macierzy łańcuchowej czwórnika, można odwzorować za

pomocą co najmniej trzech gałęzi impedancyjnych. Jeżeli impedancje te są

połączone w gwiazdę otrzymujemy schemat zastępczy, który można

narysować w kształcie litery T (rys.2).Schemat taki nazywamy schematem

typu T. Jeśli impedancje są połączone w trójkąt, otrzymujemy schemat

zastępczy, który można narysować w kształcie litery

π (rys.3).Schemat taki

nazywamy schematem typu

π.

Rys.2 Schemat zastępczy czwórnika typu T

Z

1

Z

2

Y

I

2

U

2

I

1

U

1

9

Rys.3 Schemat zastępczy czwórnika typu

π

Czwórnik typu T.

W odniesieniu do czwórnika typu T wyznaczamy zależność pomiędzy

parametrami łańcuchowymi a elementami czwórnika.

Na podstawie drugiego prawa Kirchhoffa dla obwodu pokazanego na rys.2

U

1

=U

2

+Z

2

I

2

+Z

1

I

1

(I.7.1)

Na podstawie pierwszego prawa Kirchhoffa

I

1

=I

2

+(U

2

+Z

2

I

2

)Y=Y U

2

+(1+Z

2

Y)I

2

(I.7.2)

W powyższym równaniu współczynnik przy U

2

jest parametrem C, a

współczynnik przy I

2

parametrem D, czyli

C=Y ;

D=1+Z

2

Y

(I.7.3)

Eliminując w pierwszym równaniu prąd I

1

i uwzględniając równanie drugie

otrzymamy

U

1

=(1+Z

1

Y)U

2

+(Z

1

+Z

2

+Z

1

Z

2

Y)I

2

(I.7.4)

W powyższym równaniu współczynnik przy U

2

jest parametrem A,

a współczynnik przy I

2

jest parametrem B, czyli

A=1+Z

1

Y ; B=Z

1

+Z

2

+Z

1

Z

2

Y

(I.7.5)

Macierz parametrów łańcuchowych czwórnika typu T ma zatem postać

A

T

=

⎥

⎦

⎤

⎢

⎣

⎡

+

+

+

+

Y

Z

Y

Y

Z

Z

Z

Z

Y

Z

2

2

1

2

1

1

1

1

(I.7.6)

Z

I

1

U

1

Y

1

I

2

U

2

Y

2

10

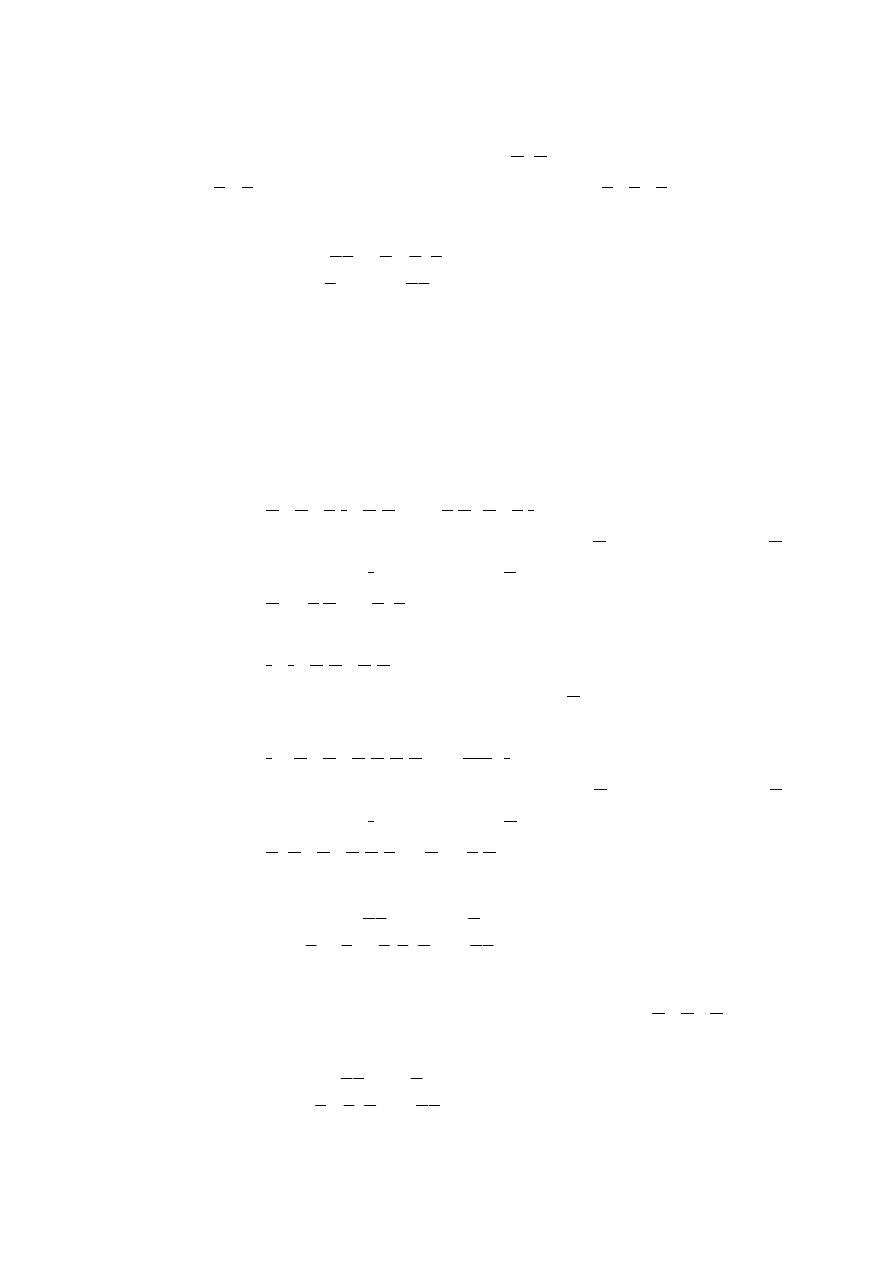
Łatwo sprawdzić,

że jest spełniony warunek odwracalności

detA

T

=1.Natomiast warunek symetrii A=D jest spełniony wówczas, gdy

Z

1

=Z

2

. Ze schematu czwórnika widać, że przy Z

1

=Z

2

=Z, czwórnik jest

symetryczny. Macierz parametrów łańcuchowych ma wtedy postać:

A

T

=

⎥

⎦

⎤

⎢

⎣

⎡

+

+

+

Y

Z

Y

Y

Z

Z

Y

Z

1

2

1

2

(I.7.7)

Czwórnik typu

π.

W odniesieniu do czwórnika typu

π, podobnie jak dla czwórnika typu T,

wyznaczymy zależności pomiędzy parametrami łańcuchowymi elementami

czwórnika.

Na podstawie drugiego prawa Kirchhoffa dla obwodu pokazanego na rys.3

U

1

=U

2

+Z(I

2

+Y

2

U

2

)=(1+Z Y

2

)U

2

+Z I

2

(I.7.8)

W powyższym równaniu współczynnik przy U

2

jest parametrem A,

a współczynnik przy I

2

jest parametrem B, czyli

A=1+Z Y

2

; B=Z

(I.7.9)

Na podstawie pierwszego prawa Kirchhoffa

I

1

=I

2

+Y

2

U

2

+Y

1

U

1

(I.7.10)

Eliminując w powyższym równaniu napięcie U

1

i uwzględniając pierwsze

równanie otrzymamy

I

1

=(Y

1

+Y

2

+Y

1

Y

2

U)U

2

+(1+Z U

1

)I

2

(I.7.11)

W powyższym równaniu współczynnik przy U

2

jest parametrem C,

a współczynnik przy I

2

jest parametrem D, czyli

C=Y

1

+Y

2

+Y

1

Y

2

Z ; D=1+Z Y

1

(I.7.12)

Macierz parametrów łańcuchowych czwórnika typu

π ma zatem postać

A

π

=

⎥

⎦

⎤

⎢

⎣

⎡

+

+

+

+

1

2

1

2

1

2

1

1

Y

Z

Z

Y

Y

Y

Y

Z

Y

Z

(I.7.13)

Łatwo można wykazać, że spełniony jest warunek odwracalności:

detA

π

=1.Warunek symetrii jest spełniony wówczas, gdy Y

1

=Y

2

=Y.Macierz

parametrów łańcuchowych ma wtedy postać:

A

π

=

⎥

⎦

⎤

⎢

⎣

⎡

+

+

+

Y

Z

Z

Y

Y

Z

Y

Z

1

2

1

2

(I.7.14)

11

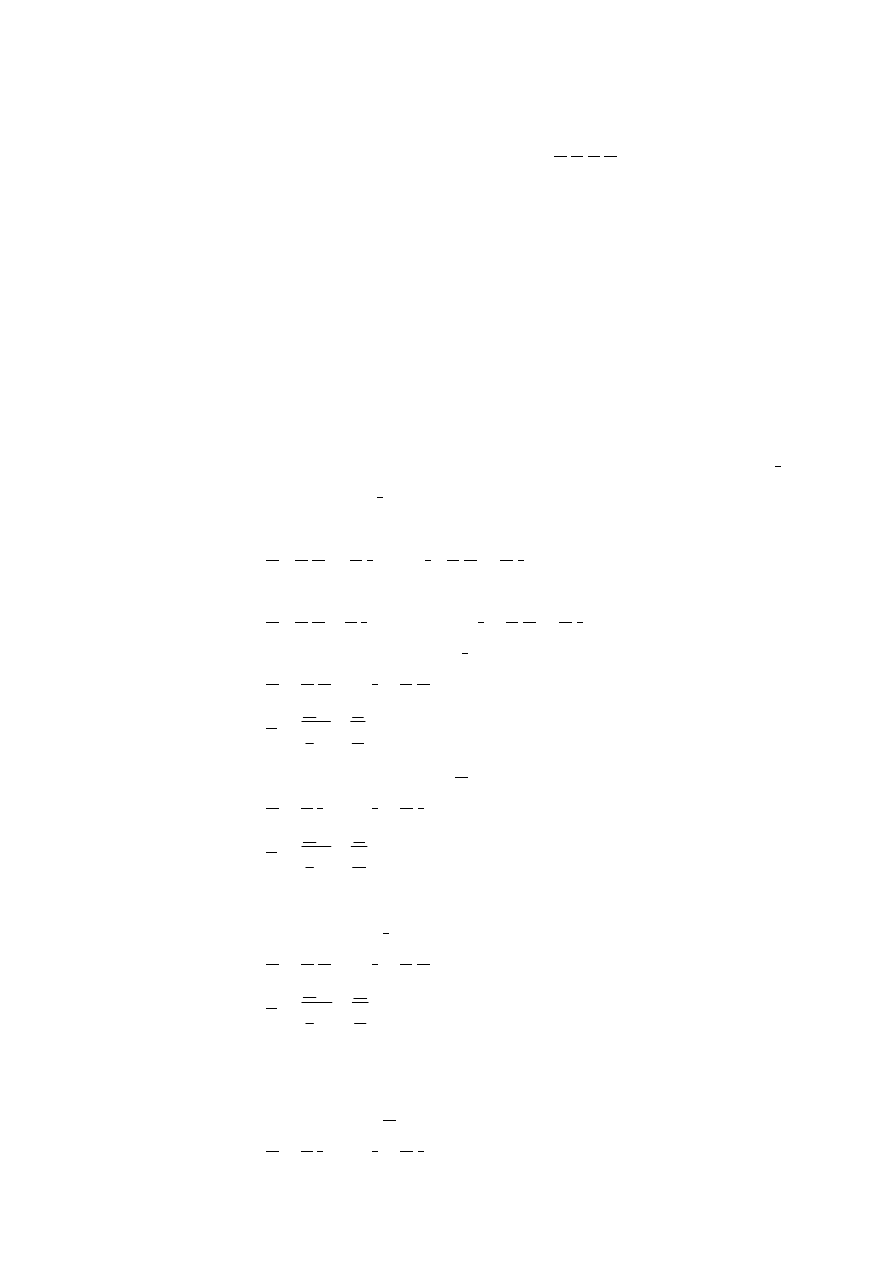
2) Wyznaczenie parametrów łańcuchowych A,B,C,D w funkcji impedancji

w stanie jałowym i w stanie zwarcia.

Gdy nie jest znana struktura wewnętrzna czwórniak pasywnego, a dostępne są

tylko jego zaciski, lub gdy schemat jest dość skomplikowany i wyznaczenie

parametrów łańcuchowych wymaga rozwiązania dużej liczby równań,

posługujemy się impedancjami w stanie jałowym i w stanie zwarcia, które są

powiązane z parametrami łańcuchowymi. Impedancje w stanie jałowym i w

stanie zwarcia można niekiedy zmierzyć i wtedy metoda, przedstawiona

poniżej, jest bardzo dogodna.

Napiszmy równanie łańcuchowe czwórnika pasywnego przy zwrotach prądu I

1

do „pudełka”, a prądu I

2

od „pudełka”:

Zgodnie z równaniem (I.3.1)

U

1

=A U

2

+ B I

2

;

I

1

=C U

2

+ D I

2

(I.7.15)

a zgodnie z równaniem (I.3.4)

U

2

=D U

1

- B I

1

;

I

2

=-C U

1

+ A I

1

(I.7.16)

W stanie jałowym zacisków 2-2’ (I

2

=0), zgodnie z (I.7.15)

U

10

=A U

2

;

I

10

=C U

2

Z

10

=

C

A

I

U

=

10

10

(I.7.17)

W stanie zwarcia zacisków 2-2’ (U

2

=0), zgodnie z (I.7.15)

U

1k

=B I

2

;

I

1k

=D I

2

Z

1k

=

D

B

I

U

k

k

=

1

1

(I.7.18)

W stanie jałowym zacisków 1-1’, przy dołączeniu źródła do zacisków 2-2’,

zgodnie z (I.7.16) przy I

1

=0

U

20

=D U

1

; I

20

=C U

1

Z

20

=

C

D

I

U

=

20

20

(I.7.19)

W stanie zwarcia zacisków 1-1’, przy dołączeniu źródła do zacisków 2-2’,

zgodnie z (I.7.16) przy U

1

=0

U

2k

=B I

1

;

I

2k

=A I

1

12

Z

2k

=

A

B

I

U

k

k

=

2

2

(I.7.20)

Do równania

A D – B C=1

Podstawiamy na podstawie zależności (I.7.20) B=A Z

2k

oraz na podstawie

zależności (I.7.19) C=

20

Z

D

, przez co otrzymujemy

1

20

2

=

−

Z

Z

D

A

D

A

k

(I.7.21)

skąd

20

2

1

1

Z

Z

D

A

k

−

=

(I.7.22)

Z zależności podanych poprzednio wynika, że

k

k

Z

Z

Z

Z

D

A

2

1

20

10

=

=

(I.7.23)

zatem

k

Z

Z

Z

A

2

20

10

2

−

=

(I.7.24)

a ostatecznie otrzymamy

A=

k

Z

Z

Z

2

20

10

−

(I.7.25)

Po wyznaczeniu parametru A możemy określić pozostałe parametry

łańcuchowe:

B=A Z

2k

(I.7.26)

C=

10

Z

A

(I.7.27)

D=A

10

20

Z

Z

(I.7.28)

Z równania (I.7.23) wynika, że dla czwórnika symetrycznego, przy A=D

Z

10

=Z

20

;

Z

1k

=Z

2k

Przy przebiegach sinusoidalnych impedancje jałowe i zwarciowe są liczbami

zespolonymi, a w ogólnym przypadku posługujemy się transformatami.

13

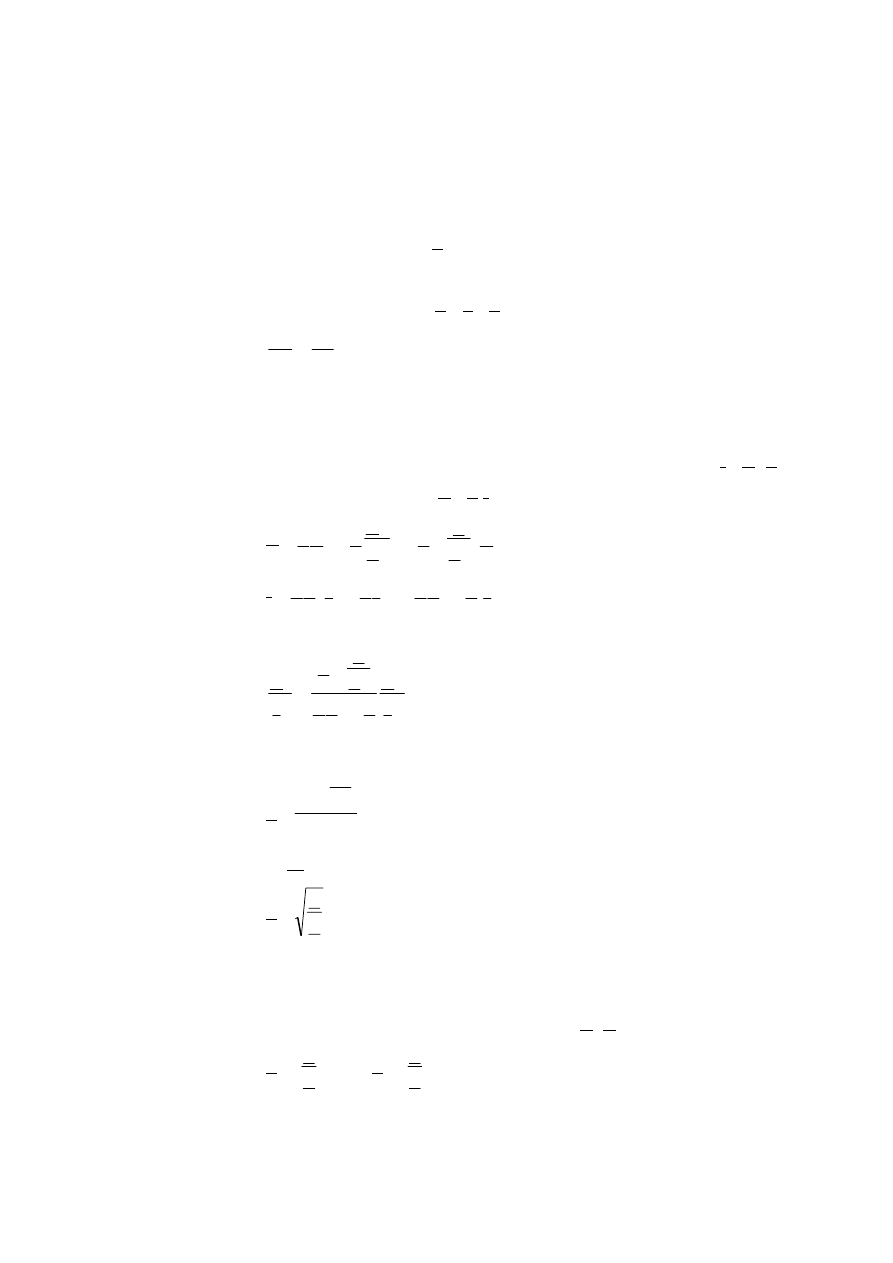
3) Impedancja charakterystyczna czwórnika symetrycznego.

Impedancją falową lub charakterystyczną czwórnika symetrycznego

nazywamy taką impedancję Z

c

, która dołączona do zacisków wyjściowych

czwórnika powoduje, że impedancja wejściowa jest jej równa.

Jeśli więc, zgodnie z definicją Z

o

=Z

c

=Z

we

to jest spełniony warunek

c

Z

I

U

I

U

=

=

1

1

2

2

(I.7.29)

Wyznaczmy teraz impedancję charakterystyczną czwórnika w funkcji jego

parametrów łańcuchowych. Równania czwórnika symetrycznego napiszmy

w postaci łańcuchowej i w równaniu pierwszym wyraźmy prąd I

2

=U

2

/Z

c

,

a w równaniu drugim napięcie U

2

=Z

c

I

2

. Zatem

U

1

=

2

2

2

U

Z

B

A

Z

U

B

U

A

c

c

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

=

+

(I.7.30)

I

1

=

(

)

2

2

2

I

A

Z

C

I

A

I

Z

C

c

c

+

=

+

(I.7.31)

Podzielmy obustronnie równanie (I.7.30) przez równanie (I.7.31)

2

2

1

1

I

U

A

Z

C

Z

B

A

I

U

c

c

+

+

=

(I.7.32)

uwzględniając zależność (I.7.29) otrzymamy

Z

c

=

c

c

c

Z

A

CZ

Z

B

A

+

+

(I.7.33)

Stąd przy C

≠ 0

Z

c

=

C

B

(I.7.34)

Impedancję charakterystyczną czwórnika symetrycznego można też uzależnić

od impedancji wejściowej czwórnika w stanie jałowymi w stanie zwarcia.

Skorzystajmy z równań (I.5.4) i (I.5.5), które przy D=A mają postać

Z

10

=

C

A

;

Z

1k

=

A

B

(I.7.35)

Po pomnożeniu stronami powyższych równań otrzymujemy

14

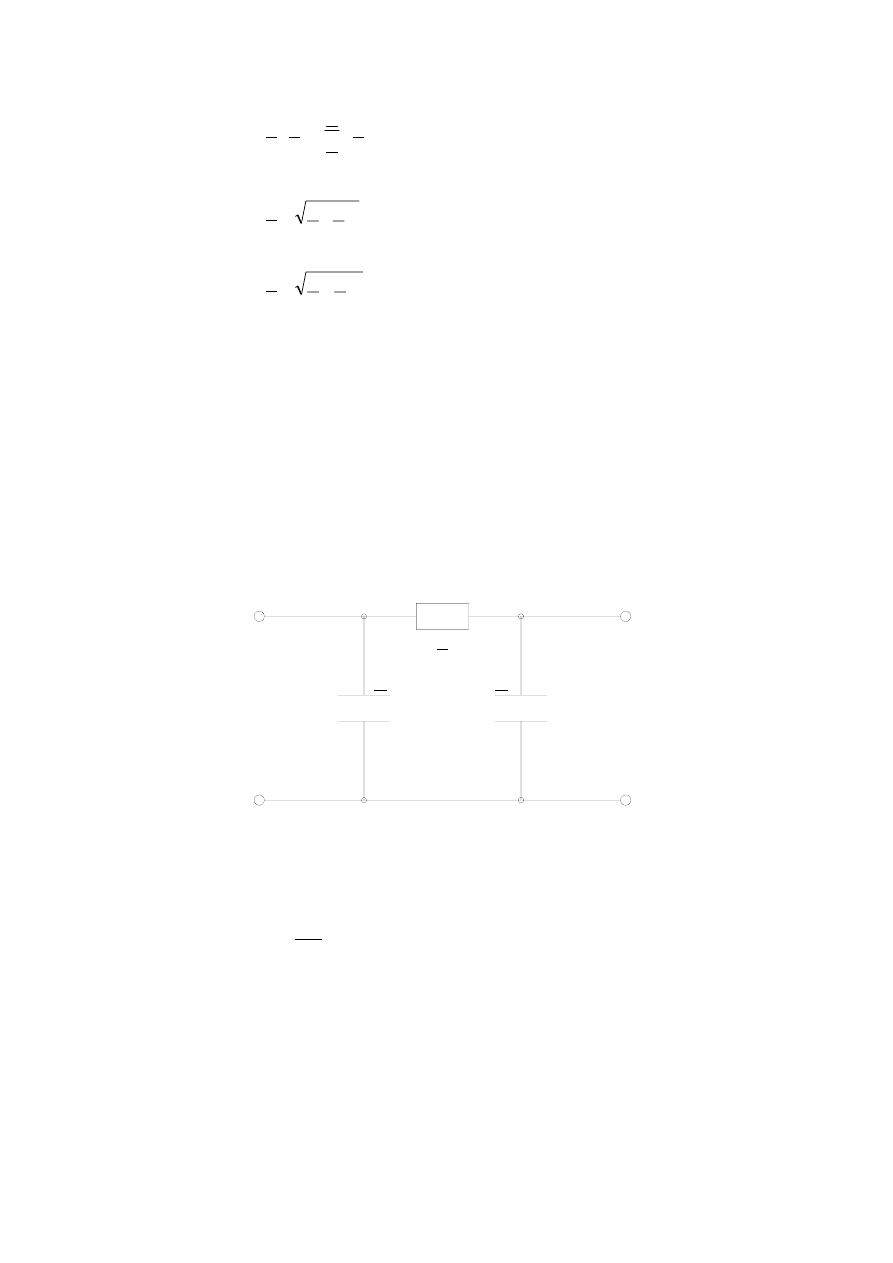
Z

10

Z

1k

=

C

B

=Z

c

2

(I.7.36)

czyli

Z

c

=

k

Z

Z

1

10

(I.7.37)

lub

Z

c

=

k

Z

Z

2

20

(I.7.38)

II. Przebieg ćwiczenia.

1. Wyznaczenie parametrów czwórnika na podstawie znajomości

impedancji elementów jego struktury.

Z

Y Y

Rys.4.Schemat badanego czwórnika

Z=R

Y=

ωC, X=

C

ω

1

,

ω=2πf

Pomiaru impedancji elementów struktury czwórnika dokonuje się w układzie

wg Rys.5 przy założeniu, że rezystancja woltomierza R

v

jest wielokrotnie

większa od impedancji elementów czwórnika

R

v

>>R ;

R

v

>>X

15

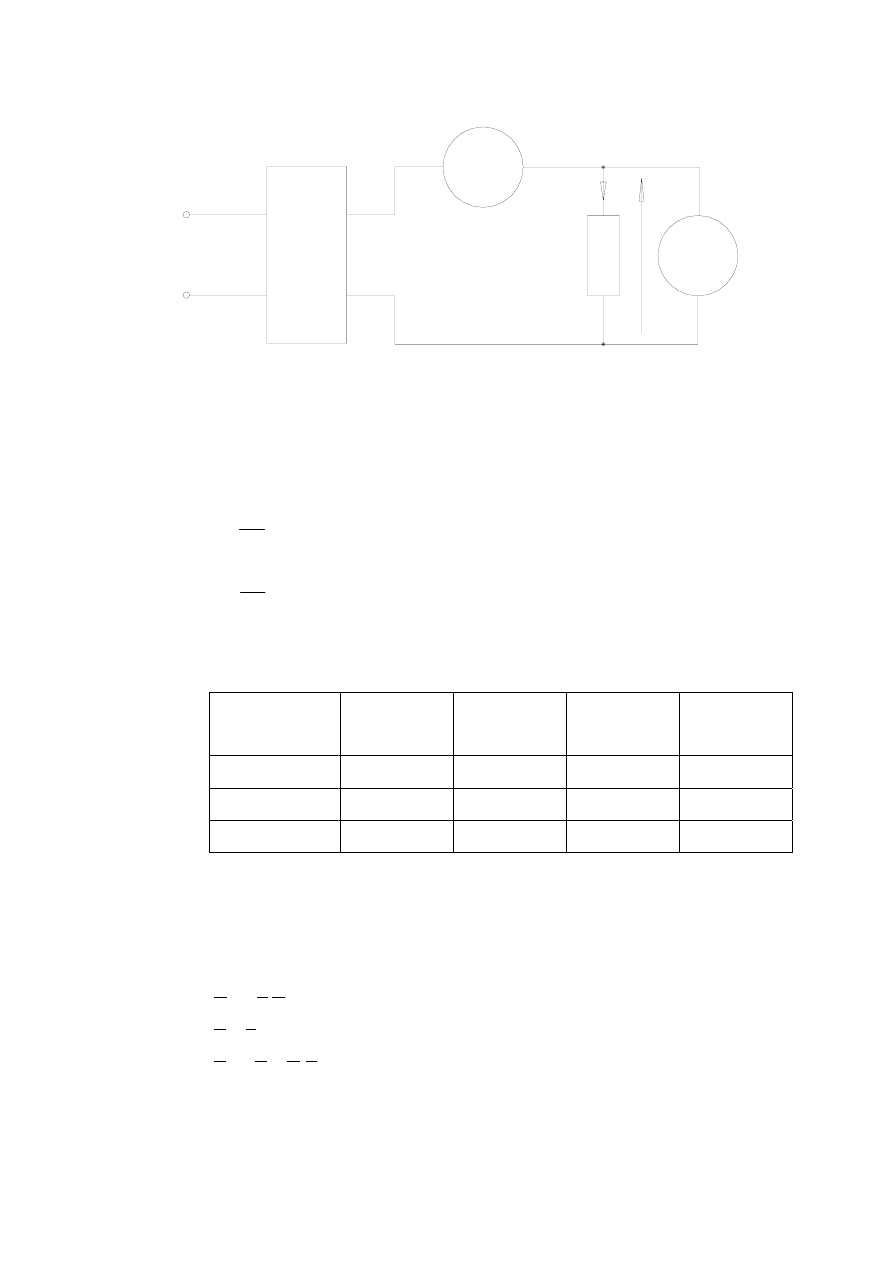
A

TRANSFO

R

M

ATOR

I U

V

∼

Rys.5 Schemat układu pomiarowego

(prostokąt symbolizuje element badany – tu: opornik lub kondensator)

Z pomiaru U, oraz I oblicza się:

R=

R

R

I

U

(układ zasilany prądem stałym)

Y=

Y

Y

U

I

(układ zasilany prądem zmiennym)

A wyniki umieszcza się w tabeli nr 1.

Obiekt

pomiaru

U I R Y

jednostka V A

Ω

S

opornik

-

kondensator

-

Tabela nr 1.

Następnie przy pomocy poniższych wzorów obliczamy parametry łańcuchowe

czwórnika i impedancje wejścia wg wzorów :

A=1+Z Y = 1 + jRC

ω = D

B = Z =R

C = 2Y + Y

2

Z =j2C

ω - R(Cω)

2

ω=2πf ; f=50Hz

16

Z

0

=

C

A

;

Z

k

=

A

B

Impedancję falową liczymy wg wzoru.

Z

c

=

k

Z

Z

0

2. Wyznaczenie parametrów czwórnika na podstawie znajomości

impedancji wejścia czwórnika w stanie biegu jałowego Z

o

i zwarcia

Z

k

.

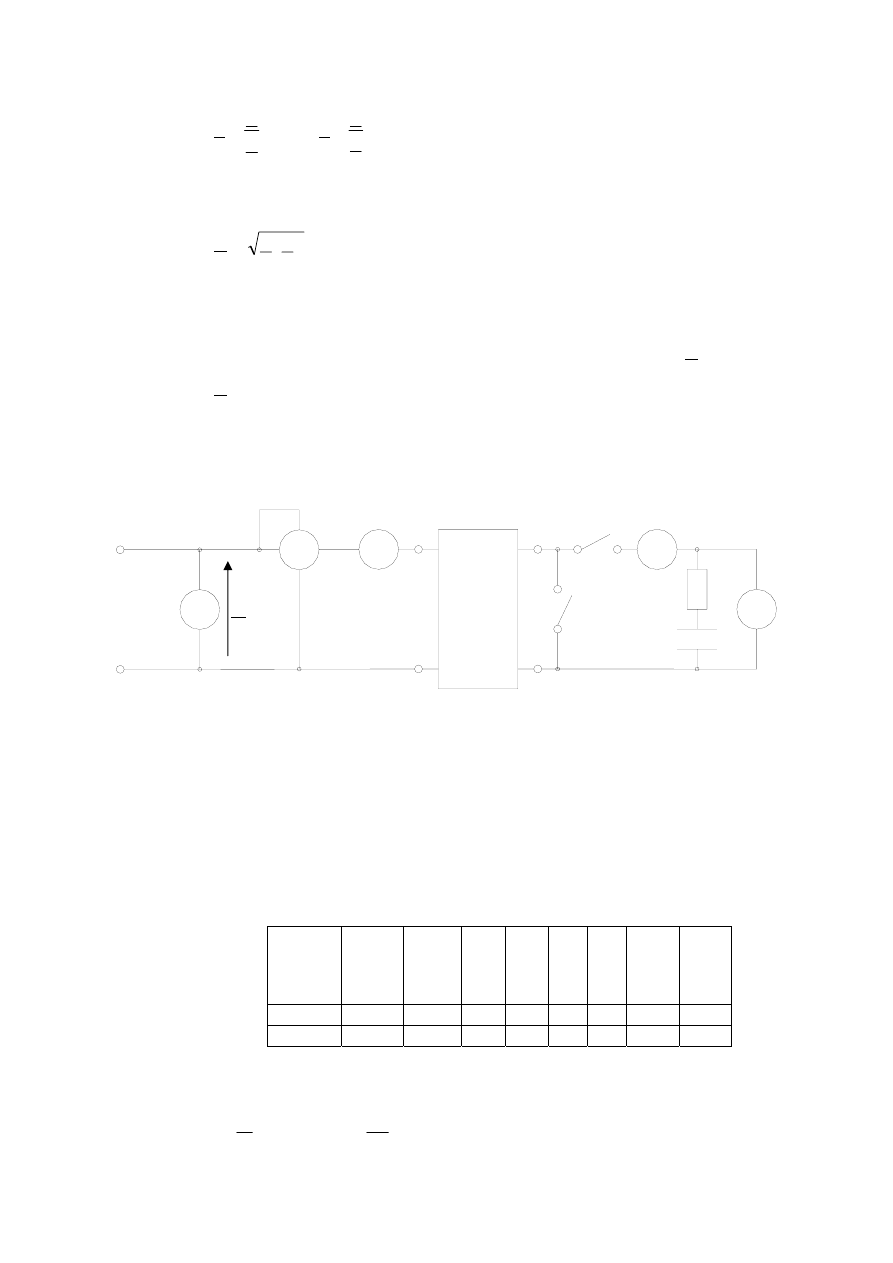
Pomiaru impedancji wejścia czwórnika dokonuje się w układzie wg Rys.6.

A

R

C

X

C

1

W A

V U

1

1`

2 K

2

K

1

2`

V

Rys.6 Schemat układu pomiarowego.

W stanie biegu jałowego czwórnika wyłącznik K

1

otwarty, w stanie zwarcia

zamknięty.

Wyniki pomiarów zapisujemy w tabeli nr 2:

Stan

czwórnika

U I P

cos

ϕ ϕ

o

ϕ

k

Z

o

Z

k

V

A

W

°

°

Ω

Ω

Jałowy

-

-

Zwarcia

-

-

Tabela nr 2

A następnie według poniższych wzorów uzupełniamy ją :

Z=

I

U

;

cos

ϕ=

UI

P

17

Z

o

=

o

j

o

e

Z

ϕ

Z

k

=

k

j

k

e

Z

ϕ

Teraz na podstawie wyników z tabeli nr 2 dokonujemy obliczenia parametrów

łańcuchowych oraz impedancji falowej czwórnika wg wzorów :

A=D=

k

Z

Z

Z

−

0

0

B=A Z

k

C=

10

Z

A

Z

c

=

k

Z

Z

0

R

c

= ReZ

c

X

c

= ImZ

c

C

c

=

ω

⋅

c

X

1

Po włączeniu na wyjściu czwórnika impedancji falowej sprawdzamy, czy

impedancje w punktach wejścia i wyjścia czwórnika są równe (przełącznik K

2

zamknięty, K

1

otwarty):

2

2

1

1

I

U

I

U =

III. Wnioski.

We wnioskach należy zamieścić własne spostrzeżenia z wykonanego ćwiczenia.

Porównać wyniki obliczeń impedancji falowej dokonanych w punkcie 1 i 2, oraz

porównać impedancję wejścia i wyjścia zmierzonych po włączeniu na wyjściu

czwórnika impedancji falowej.

IV. Literatura.

Elektrotechnika teoretyczna – Maciej Krakowski
Elektrotechnika teoretyczna – Stanisław Bolkowski
Elektrotechnika – Eugeniusz Nieciejowski

18